I whined on IRC about my inability to do simple trig and dakkar kindly
took me through the basics of a cosine. So I sat down later to look
again at an exercise I'd skipped: 2.2 to defined the function:
> regularPolygon :: Int -> Side -> Shape>
But I realised that I still couldn't remember what I was doing and so
consulted Wikipedia's handy page on trigonometry. Armed with Cos A =
adjacent/hypotenuse I knocked together
> regularPoly :: Int -> Float -> Shape
> regularPoly nsides r = Polygon $ _poly
> where _poly :: Int -> [(Float,Float)]
> _poly side
> = let frac = 1 / fromIntegral nsides
> xyRay :: Int -> (Float,Float)
> xyRay side =
> let ratio = frac * fromIntegral side
> rad = ratio * 2*pi
> adj = cos rad * r
> opp = sin rad * r
> in (adj, opp)
> in if side == nsides then []
> else xyRay side : _poly (side+1)
OK, so this is certainly baby-Haskell, but I was quite pleased with it.
I'm liking let clauses, which is interesting, coming from Perl 5
where lexical subs don't exist and so I never saw the need for them
before. I'm finding that where clauses have slightly different
scoping rules (I had to move the definition of xyRay into a let as it
didn't work as a where. Then I realized that _poly on the other hand
would work in a where as well as a let).
To check if it worked, I plugged it into the code for chapter 4, first of all forgetting to add
regularPoly to the list of functions exported by Shape.hs. The
function works fine, though I've realised now it's not to specification
- it takes a “radius†rather than the length of the side. Sigh,
I'll come back to that problem later.
… (some time later)
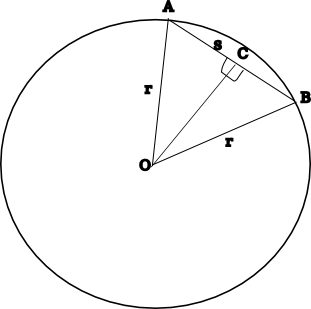
The line AB is of length s, which is how the input is
specified. We're using r instead. Bisecting the line, we have
2 triangles with perpendicular sides s/2 and r. The
angle AOB is of 360/n where n is the number
of sides. So AOC is 180/n. Using the tangent
identity:
> tan 180/n = s/2 / r
> s = 2r * tan 180/n
> r = s/(2 * tan 180/n)
So in Haskell, we can define a facade on regularPoly like so:
> -- #sides -> side -> Polygon [(x,y)]
> regularPoly2 :: Int -> Float -> Shape
> regularPoly2 nsides s = regularPoly nsides r
> where r = s / (2 * tan (pi / fromIntegral nsides))
Then of course, on IRC, Apocalisp showed his version of it which is
significantly more beautiful, and which uses the clever idea of rotating
a point an infinite number of times and then take‘ing from it.
I asked permission to post it here, which he gave, but then told me that
there was a bug in it for larger polygons, which could just be to do
with floating point precision so he was proving it correct first.
Which is the kind of rigour that I'm quite manifestly lacking.
I have an up-to-date version of his code now, but I think I'll do a
proper analysis of his and David's versions of a couple of answers and
possibly (eeeek!) try to prove them correct/equivalent.